Article: Establishing Trust in Wearable Medical Devices

Many of the topics covered in this article I have covered in this blog. Most recently, my discussion of signal detection and the Apple Watch (https://medicalremoteprogramming.blogspot.com/2019/12/signal-detection-and-apple-watch.html) that I suggest that you read after reading this article from Machine Design.

Here's the link to the article: https://www.machinedesign.com/medical-design/article/21122718/establishing-trust-in-healthcare-wearables?utm_source=MN+MD+Medical+Design&utm_medium=email&utm_campaign=CPS200206038&o_eid=7596G0176945B2B&rdx.ident%5Bpull%5D=omeda%7C7596G0176945B2B&oly_enc_id=7596G0176945B2B

Here are a few quotes from the article.

To say that we can get personal health insight from continuous monitoring presumes a “chain of trust.” In other words: 

• The interpretation of any data must not only be accurate but reliable. The challenge lies in handling “borderline” data. Any interpreting strategy or algorithm faces data sets that it finds ambiguous. For an algorithm to be reliable, users must be able to quantitatively understand its detection limits and error characteristics.

• The data and/or its interpretation must reliably reach the decision-maker for it to become actionable.

• The data must be correctly associated with historical records of the patient for it to have context.

• The data must be proven to be authentic to trigger any meaningful action.

However, using clinical equipment to capture vital signs that are representative of the wearable use cases is often difficult and sometimes inaccurate. To avoid a rash of false positives or false negatives, one must carefully select the population of test subjects and carefully develop the representative use cases. It’s also important to compare data from the patient’s own history or baseline, keeping in mind that this baseline isn’t static as the patient ages and undergoes other changes.

Signal Detection and the Apple Watch

In the last two articles about the Apple Watch's capability to detect atrial fibrillation, I made references to terminology ("false positive") that has its roots in Signal Detection Theory.  Signal Detection Theory was developed as a means to determine the accuracy of early radar systems. The technique has migrated to communications systems, psychology, diagnostics and a variety of other domains where determining the presence or absence of something of interest is important especially when the signal to be detected would be presented within a noisy environment (this was particularly true of  early radars) or when the signal is weak and difficult to detect.  

Signal detection can be powerful tool to guide research methodologies and data analysis. I have used the signal detection paradigm in my own research both for the development of my research methodology and data analysis: planned and post-hoc analysis. In fact when I have taught courses in research methods and statistical analysis, I have used the signal detection paradigm as a way to convey detecting the effects of an experimental manipulation in your data.  

Because I've mentioned issues related to signal detection and that it is a powerful tool for research and development, I decided to provide a short primer of signal detection.

Signal Detection

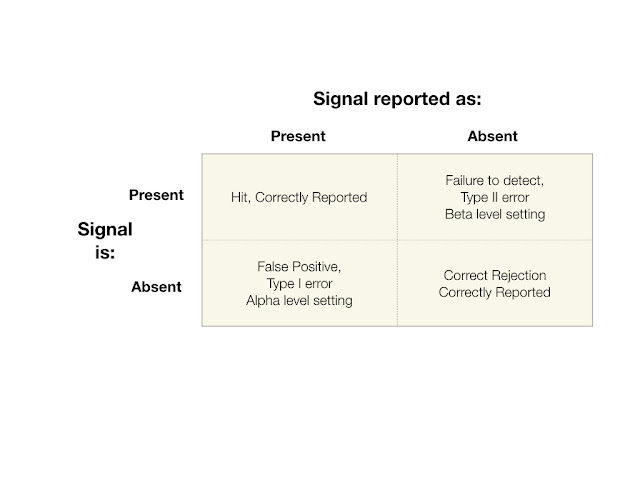
The central feature of signal detection is the two by two matrix shown below.

The signal detection process begins with a detection window or event. The window for detection could be a period of time or a specified occurrence such as a psychological test such as a rapid presentation of a stimulus and determine whether or not the subject of the experiment detected what was presented. 

Or in the case of the Apple Watch, whether it detects atrial fibrillation. In devices such as the Apple Watch, how the system defines the detection window can be important. Since we have no information regarding how the Apple Watch atrial fibrillation detection system operates, it's difficult to determine how it determines its detection window.

Multiple, Repeated Trials

Before discussing the meaning of the Signal Detection Matrix, it's important to understand that every matrix comes with multiple, repeated trials with a particular detection system, whether that detection system is a machine or a biological entity such as a person. Signal Detection Theory is grounded in probability theory, therefore, there is the requirement for multiple trials in order to create a viable and valid matrix.

The Four Cells of the Signal Detection Matrix

During the window of detection, a signal may or may not be present. Each cell represents an outcome of a detection event. The possible outcomes are: 1: the signal was present and it was detected, a hit (upper left cell), 2: the signal was not present and the system or person correctly correctly reported no signal present (lower right cell), 3: the signal was absent, but erroneously reported as present, this is a Type I error (lower left cell) and 4: the signal was present, but reported as absent, this is a Type II error (upper right cell).

The object of any system is that the outcomes of detection events end up in outcome cells 1 and 2, that is, correctly reported. However, from a research standpoint, the error cells (Outcomes 3 and 4) are the most interesting and revealing. 

Incorrect Report: Cells

Outcome 3: Type I Error

A Type I error is reporting that a signal is present when it was not. This is known as a "false alarm or false positive." The statistic for alpha which is the ratio of Outcome 3 over Total number of trials or detection events.

Outcome 4: Type II Error

A Type II error is reporting that a signal is not present when in fact it was present. This is a "failure to detect." The statistic for beta which is the ratio of Outcome 4 over Total number of trials or detection events. 


If you're designing a detection system, the idea is to minimize both types of errors. However, no system is perfect and as such, it's important to determine what type of error is most acceptable, Type I or II because there are likely to be consequences either way. 

Trade-off Between Type I and Type II Errors

In experimental research the emphasis has largely been on minimizing Type I errors, that is reporting an experimental effect when in actuality none was present. Increasing your alpha level, that is decreasing your acceptance of Type I errors, increases the likelihood of making a Type II error, reporting that an experimental effect was not present when in fact it was. 

However, with medical devices, what type of error is of greater concern, Type I or Type II? That's a decision that will need to be made.

Before leaving this section, I should mention that the trade-off analysis between Type I and Type II errors is called Receiver-Operating-Characteristic Analysis or ROC-analysis. This is something that I'll discuss in a later article. 

With Respect to the Apple Watch 

Since I have no access into Apple's thinking when it was designing the Watch's atrial fibrillation software system, I can't know for certain the thinking that went into designing atrial fibrillation detection algorithm for the Apple Watch. However based on their own research, it seems that Apple made the decision to side on accepting false positives over false negatives -- although we can't be completely sure this is true because Apple did not do the research to determine rate that the Apple Watch failed to detect atrial fibrillation when it was know to be present.

With a "medical device" such as the Apple Watch, it would seem reasonable to side on accepting false positives over false positive. That is, to set your alpha level low. The hope would be that if the Apple Watch detected atrial fibrillation the owner of the watch would seek medical attention to determine whether or not a diagnosis of atrial fibrillation was warranted for receiving treatment for the condition. If the watch generated a false alarm, then there was no harm in seeking medical advice ... it would seem. The author of the NY Times article I cited in the previous article appears to hold to this point of view. 

However ...

The problem with a system that generates a high rate of false alarms, is that all too often signals tend to be ignored. Consider the following scenario: an owner of an Apple Watch receives an indication that atrial fibrillation has been detected. The owner goes to a physician who reports that there's no indication of atrial fibrillation. Time passes and the watch reports again that atrial fibrillation has been detected. The owner goes back to the physician who give the owner the same report as before, no atrial fibrillation detected. What do you think will happen if the owner receives from the watch that atrial fibrillation has been detected? It's likely that the owner will just ignore the report. That would really be a problem for the owner if the owner had in fact developed atrial fibrillation. In this scenario the watch "cried wolf" too many times. And therein lies the problem with having a system that's adjusted to accepting a high rate of false alarms.

Follow-up: Apple Watch 5, Afib detection, NY Times Article

The New York Times has published an article regarding the Apple Watch 5's capability to detect atrial fibrillation. The link to the article is below:

https://www.nytimes.com/2019/12/26/upshot/apple-watch-atrial-fibrillation.html?te=1&nl=personal-tech&emc=edit_ct_20191226?campaign_id=38&instance_id=14801&segment_id=19884&user_id=d7e858ffd01b131c28733046812ca088&regi_id=6759438320191226

The title and the subtitle of the article provide a good summary of what the author (Aaron E. Carroll) found:

"The Watch Is Smart, but It Can’t Replace Your Doctor
Apple has been advertising its watch’s ability to detect atrial fibrillation. The reality doesn’t quite live up to the promise."

With reference to my article, the Times article provides more detail on the trial that Apple ran to test the effectiveness of the Apple Watch's ability to detect atrial fibrillation. That provide interesting and enlightening, and clarified some of the issues I found with how the study was reported for both the procedure and the results. In addition, the author and I concur regarding the Apple Watch's extremely high reported rate of false positives for atrial fibrillation. I find this quite interesting when you consider that screening for atrial fibrillation can be as simple as taking the patient's pulse. 

Here are a few quotes from the article:

"Of the 450 participants [these are study participants where the Apple Watch had detected atrial fibrillation] who returned patches , atrial fibrillation was confirmed in 34 percent, or 153 people. 
...

Many news outlets reporting on the study mentioned a topline result: a “positive predictive value” of 84 percent. That statistic refers to the chance that someone actually has the condition if he or she gets a positive test result.

But this result wasn’t calculated from any of the numbers above. It specifically refers to the subset of patients who had an irregular pulse notification while wearing their confirmatory patch. That’s a very small minority of participants. Of the 86 who got a notification while wearing a patch, 72 had confirmed evidence of atrial fibrillation. (Dividing 72 by 86 yields 0.84, which is how you get a positive predictive value of 84 percent.)

Positive predictive values, although useful when talking to patients, are not always a good measure of a test’s effectiveness. When you test a device on a group where everyone has a disease, for instance, all positive results are correct."
...

There are positive messages from this study. There’s potential to use commercial devices to monitor and assess people outside of the clinical setting, and there’s clearly an appetite for it as well. But for now and based on these results, while there may be reasons to own an Apple Watch, using it as a widespread screen for atrial fibrillation probably isn’t one."